[PlayData - Day 9] Numpy - 배열 데이터 다루기

1. K-Digital Training 과정

• 빅데이터 기반 지능형SW 및 MLOps 개발자 양성과정 19기 (2023/01/02 - Day 9)

2. 목차

1. 배열 생성하기
2. 배열의 연산
3. 배열의 인덱싱과 슬라이싱

3. 수업 내용

1. 배열 생성하기

import numpy as np

arr_abj = np.array(seq_data)
시퀀스 데이터(seq_data)를 인자로 받아 NumPy의 배열 객체(array object)를 생성
리스트와 튜플 타입의 데이터를 모두 사용할 수 있지만 주로 리스트 데이터를 이용

data1 = [0,1,2,3,4,5]
a1 = np.array(data1)
a1

>>> array([0, 1, 2, 3, 4, 5])

data2 = [0.1, 5, 4, 12, 0.5]
a2 = np.array(data2)
a2

>>> array([ 0.1,  5. ,  4. , 12. ,  0.5])

a1.dtype

>>> dtype('int32')

a2.dtype

>>> dtype('float64')

np.array([0.5, 2, 0.01, 8])

>>> array([0.5 , 2.  , 0.01, 8.  ])

np.array([[1,2,3,], [4,5,6], [7,8,9]])

>>> array([[1, 2, 3],
>>>        [4, 5, 6],
>>>        [7, 8, 9]])

범위를 지정해 배열 생성

arr_obj = np.arrange([start,] stop[, step])

np.arange(0, 10, 2) # 0에서 10까지 2 step으로

>>> array([0, 2, 4, 6, 8])

np.arange(1, 10) # 1에서 10까지 1 step으로

>>> array([1, 2, 3, 4, 5, 6, 7, 8, 9])

np.arange(5) # 0에서 5까지 1step으로

>>> array([0, 1, 2, 3, 4])

.reshape(m,n)을 추가하면 m x n 형태의 2차원 배열(행렬)로 변경할 수 있다.
행과 열의 위치는 각각 0부터 시작

np.arange(12).reshape(4,3)

>>> 
array([[ 0,  1,  2],
       [ 3,  4,  5],
       [ 6,  7,  8],
       [ 9, 10, 11]])

arange()로 생성되는 배열의 원소 개수와 reshape(m,n)의 m x n 개수는 같아야 한다.

b1 = np.arange(12).reshape(4,3)
b1.shape

>>> (4, 3)

b2 = np.arange(5)
b2.shape             # n개의 요소를 갖는 1차원 배열의 경우에는 'ndarray.shape'를 수행하면 '(n,)'처럼 표시된다.

>>> (5,)

arr_obj = np.linspace(start, stop[, num])
start부터 stop까지 num개의 NumPy 배열을 생성
num을 지정하지 않으면 50으로 간주

np.linspace(1, 10, 10)

>>> array([ 1.,  2.,  3.,  4.,  5.,  6.,  7.,  8.,  9., 10.])

np.linspace(1, 10, 19) # 일정한 간격으로 나눠준다.

>>> array([ 1. ,  1.5,  2. ,  2.5,  3. ,  3.5,  4. ,  4.5,  5. ,  5.5,  6. ,
>>>         6.5,  7. ,  7.5,  8. ,  8.5,  9. ,  9.5, 10. ])

np.linspace(0, np.pi, 20)

>>> array([0.        , 0.16534698, 0.33069396, 0.49604095, 0.66138793,
>>>        0.82673491, 0.99208189, 1.15742887, 1.32277585, 1.48812284,
>>>        1.65346982, 1.8188168 , 1.98416378, 2.14951076, 2.31485774,
>>>        2.48020473, 2.64555171, 2.81089869, 2.97624567, 3.14159265])

특별한 형태의 배열 생성

arr_zero_n = np.zeros(n)
arr_zero_mxn = np.zeros((m,n))
arr_one_n = np.ones(n)
arr_one_mxn = np.ones((m,n))

np.zeros(10)

>>> array([0., 0., 0., 0., 0., 0., 0., 0., 0., 0.])

np.zeros((3,4))

>>> array([[0., 0., 0., 0.],
>>>        [0., 0., 0., 0.],
>>>        [0., 0., 0., 0.]])

np.ones(5)

>>> array([1., 1., 1., 1., 1.])

np.ones((3, 5))

>>> 
array([[1., 1., 1., 1., 1.],
       [1., 1., 1., 1., 1.],
       [1., 1., 1., 1., 1.]])

arr_I = np.eye(n)
단위행렬(Identity matrix) 생성: n x n인 정사각형 행렬에서 주 대각선이 모두 1이고 나머지는 0인 행렬

np.eye(3)

>>> 
array([[1., 0., 0.],
       [0., 1., 0.],
       [0., 0., 1.]])

배열의 데이터 타입 변환

NumPy의 배열은 숫자뿐만 아니라 문자열도 원소로 가질 수 있다
num_arr = str_arr(astype(dtype))

np.array(['1.5', '0.62', '2', '3.14', '3.141592'])

>>> array(['1.5', '0.62', '2', '3.14', '3.141592'], dtype='<U8')

기호	의미
'b'	불, bool
'i'	기호가 있는 정수, (signed) integer
'u'	기호가 없는 정수, unsigned integer
'f'	실수, floating-point
'c'	복소수, complex-floating point
'M'	날짜, datetime
'O'	파이썬 객체, (Python) objects
'S' 혹은 'a'	바이트 문자열, (byte) string
'U'	유니코드, Unicode

str_a1 = np.array(['1.567', '0.123', '5.123', '9', '8'])
num_a1 = str_a1.astype(float)
num_a1

>>> array([1.567, 0.123, 5.123, 9.   , 8.   ])

str_a1.dtype

>>> dtype('<U5')

num_a1.dtype

>>> dtype('float64')

str_a2 = np.array(['1','3','5','7','9'])
num_a2 = str_a2.astype(int)
num_a2

>>> array([1, 3, 5, 7, 9])

str_a2.dtype

>>> dtype('<U1')

num_a2.dtype

>>> dtype('int32')

실수를 정수로

num_f1 = np.array([10,21,0.549,4.75,5.98])
num_i1 = num_f1.astype(int)
num_i1

>>> array([10, 21,  0,  4,  5])

2. 배열의 연산

기본 연산

배열의 형태가 같다면 연산이 가능

arr1 = np.array([10,20,30,40])
arr2 = np.array([1,2,3,4])

arr1 + arr2

>>> array([11, 22, 33, 44])

arr1 - arr2

>>> array([ 9, 18, 27, 36])

arr2*2

>>> array([2, 4, 6, 8])

arr2**2

>>> array([ 1,  4,  9, 16], dtype=int32)

arr1*arr2

>>> array([ 10,  40,  90, 160])

arr1/arr2

>>> array([10., 10., 10., 10.])

 

# 복합 연산
arr1/(arr2**2)

>>> array([10.        ,  5.        ,  3.33333333,  2.5       ])

# 비교 연산
arr1 > 20

>>> array([False, False,  True,  True])

통계를 위한 연산

arr3 = np.arange(5)
arr3

>>> array([0, 1, 2, 3, 4])

합계 sum()와 평균 mean()

[arr3.sum(), arr2.mean()]

>>> [10, 2.5]

표준편차 std()와 분산 var()
표준편차 = 평균을 중심으로 퍼져있는 정도
분산 = 변량이 평균으로부터 떨어져 있는 정도

[arr3.std(), arr3.var()]

>>> [1.4142135623730951, 2.0]

[arr3.min(), arr3.max()]

>>> [0, 4]

누적 합 cumsum()과 누적 곱 cumprod()

arr4 = np.arange(1,5)
arr4

>>> array([1, 2, 3, 4])

arr4.cumsum()   # cumulative sum

>>> array([ 1,  3,  6, 10], dtype=int32)

arr4.cumprod()  # cumulative product

>>> array([ 1,  2,  6, 24], dtype=int32)

행렬 연산

A = np.array([0,1,2,3]).reshape(2,2)
B = np.array([3,2,0,1]).reshape(2,2)
display(A, B)

>>> 
array([[0, 1],
       [2, 3]])

>>> 
array([[3, 2],
       [0, 1]])

행렬 곱 (matrix product)
두 개의 행렬에서 한 개의 행렬을 만들어내는 이항 연산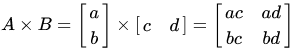

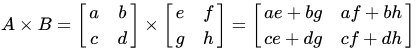
https://ko.m.wikipedia.org/wiki/행렬_곱셈

 

https://m.blog.naver.com/statstorm/221758839377

A.dot(B)

>>> 
array([[0, 1],
       [6, 7]])

np.dot(A, B)

>>> 
array([[0, 1],
       [6, 7]])

np.dot(B, A)

>>> 
array([[4, 9],
       [2, 3]])

전치 행렬 (transpose matrix)
행과 열의 위치를 바꾸는 것

np.transpose(A)

>>> 
array([[0, 2],
       [1, 3]])

A.transpose()

>>> 
array([[0, 2],
       [1, 3]])

역행렬 (reverse matrix)
행렬의 곱셈에 대한 역원
정사각행렬 A의 역행렬이란 행렬 A와 곱했을 때 단위행렬 I가 나오는 행렬이다.
정사각형 행렬 A = [[a, b,],[c, d]] 일 때,
A의 역행렬 𝐴−¹는 다음과 같다.
𝐴−¹=1/(𝑎𝑑−𝑏𝑐)[[𝑑,−𝑏],[−𝑐,𝑎]]

https://m.terms.naver.com/entry.naver?docId=3338111&cid=47324&categoryId=47324

 

https://m.terms.naver.com/entry.naver?docId=3338111&cid=47324&categoryId=47324

 

https://m.terms.naver.com/entry.naver?docId=3338111&cid=47324&categoryId=47324

np.linalg.inv(A)

>>> 
array([[-1.5,  0.5],
       [ 1. ,  0. ]])

A.dot(np.linalg.inv(A))

>>> 
array([[1., 0.],
       [0., 1.]])

# linear algebra
?np.linalg

>>> 
# inverted
?np.linalg.inv

행렬식 (determinant)

행렬식의 값이 0이면 역행렬이 존재하지 않는다. (det A = ad - bc = 0이면 A의 역행렬은 존재하지 않는다.)

np.linalg.det(A)

>>> -2.0

A

>>> 
array([[0, 1],
       [2, 3]])

-0.5*np.array([[3,-1],[-2,0]]) # == np.linalg.inv(A)

>>> 
array([[-1.5,  0.5],
       [ 1. , -0. ]])

3. 배열의 인덱싱과 슬라이싱

배열의 인덱싱

배열의 위치나 조건을 지정해 배열의 원소를 선택하는 것
배열명[위치]

a1 = np.array([0,10,20,30,40,50])
a1

>>> array([ 0, 10, 20, 30, 40, 50])

a1[0]

>>> 0

a1[4]

>>> 40

원소 변경하기: 1차원 배열. 리스트와 큰 차이가 없다.

a1[5] = 70
a1

>>> array([ 0, 10, 20, 30, 40, 70])

a1[[1,3,4]] # 특정 위치에 있는 값만 모아서 볼 때 (1, 3, 4번째 위치의 값)

>>> array([10, 30, 40])

2차원 배열 생성

a2 = np.arange(10, 100, 10).reshape(3,3)
a2

>>> 
array([[10, 20, 30],
       [40, 50, 60],
       [70, 80, 90]])

a2[0, 2] # 0+1행 2+1열

>>> 30

a2[2][2]

>>> 90

2차원에서 원소 값 변경

a2[2,2] = 95
a2

>>> 
array([[10, 20, 30],
       [40, 50, 60],
       [70, 80, 95]])

하나만 입력하면 행위치를 지정함

a2[1]

>>> array([40, 50, 60])

2차원에서 특정 행을 변경

a2[1] = np.array([45, 55, 65])
a2

>>> 
array([[10, 20, 30],
       [45, 55, 65],
       [70, 80, 95]])

a2[1] = [47,57,67]
a2 # 리스트를 이용해서도 가능하다

>>> 
array([[10, 20, 30],
       [47, 57, 67],
       [70, 80, 95]])

2차원 배열에서 여러 원소 선택하기
배열명 [행 위치1, 행 위치2, ..., 행 위치[n]], [열 위치1, 열 위치2, ..., 열 위치[n]]

a2[[0, 2], [0, 1]]

>>> array([10, 80])

배열 [조건]

a = np.array([0,1,2,3,4,5,-1])
a[a>3]

>>> array([4, 5])

짝수만 출력

a[(a%2)==0]

>>> array([0, 2, 4])

배열의 슬라이싱

범위를 지정해 배열의 일부분을 선택하는 슬라이싱
배열 [시작:끝]

b1 = np.array([0, 10, 20, 30, 40, 50])
b1[1:4]

>>> array([10, 20, 30])

b1[:3]

>>> array([ 0, 10, 20])

b1[2:]

>>> array([20, 30, 40, 50])

슬라이싱으로 원소 변경

b1[2:5] = np.array([25, 35, 45])
b1

>>> array([ 0, 10, 25, 35, 45, 50])

b1[3:6] = 60
b1

>>> array([ 0, 10, 25, 60, 60, 60])

2차 배열에서의 슬라이싱

b2 = np.arange(10, 100, 10).reshape(3,3)
b2

>>> 
array([[10, 20, 30],
       [40, 50, 60],
       [70, 80, 90]])

배열 [행시작:행끝, 열시작:열끝]

b2[1:3, 1:3]

>>> 
array([[50, 60],
       [80, 90]])

b2[:3, 1:]

>>> 
array([[20, 30],
       [50, 60],
       [80, 90]])

슬라이싱 된 배열에 값 지정하기

b2[0:2, 1:3] = np.array([[25, 35], [55, 65]])

display(b2)

>>> 
array([[10, 25, 35],
       [40, 55, 65],
       [70, 80, 90]])